まとめ:円柱の体積の求め方は楽勝すぎる! 円柱の体積の求め方はどうだったかな?? 半径×半径×円周率×高さ で円柱の体積は計算できたね。 円柱の体積を計算できるようになったらついでに円柱の表面積の求め方にもチャレンジしてみよう!<円柱貫通体について> 積分を応用して円柱貫通体の体積Vを求める。 2本の円柱が交わった部分の立体の体積を求める有名な問題でが、高校生3年生時に説明を聞くまでは、立体 の形がイメージできなかったのではないでしょうか?つまり、立体の存在自体に詐欺があります。以下に4つ の解法立体の体積を求めるには,体積の微分が断面積になることを利用します. すなわち,左端 a から座標 x までの区間にある体積を x の関数として V (x) で表し, x における断面積を S (x) とおきます. が示されます. (底辺)×(高さ h ) になる. 同様にし
Http Www Shimanet Ed Jp Minami Link Homepage Naga005 Grapes 001 Enchuu2ko Pdf
円柱 球 重なり 体積
円柱 球 重なり 体積-第5節 円柱と円錐 円錐と円柱(その1) 立体の体積を計算するのに用いる置換積分を解説することを目的に書き始めましたが,表面積, 正射影,双曲線,円錐,円柱,外積等を書き加えたため雑多な内容になりました. 各節は独立しているので,どこからでも読み始められるようになってい円錐と円柱の重なり部分の体積を求める問題です 大学入試問題なのですが、判らなくて困っています。 xyz空間内に底面がx^2+y^2≦4、z=0、頂点が(0,0,2)の円錐と、底面が(x-1)^2+y^2≦1、z=0、上面が(x-1)^2+y^2≦1、z=2の円柱がある(円錐、円柱ともに内部を含むものとする)。こ




非回転体 交差する円柱の共通部分 Steinmetz Solid 理系のための備忘録
角柱と円柱の体積 角柱の体積 問題一括 (1,476Kb) 解答一括 (1,575Kb) 円柱の体積 10 およその面積 およその面積 問題一括 (875Kb) 解答一括 (9Kb) 11 比例と反比例 比例の式 問題一括 (4,628Kb) 解答一括 (4,4Kb) 比例の性質 比例のグラフ(1) 比例のグラフ(2) 力をつけよう(1) 力をつけよう(2) 力体積における置換積分を理解していれば次の問題は難しくありません. 例題3 立体A,B,Cをそれぞれ半径の1の直円柱とする.A,B,Cのどの2つの中心軸も直交するとき, 3つの円柱の共通部分の体積3 円筒配管系統上点群の選択的自動抽出手法 前述の問題解決のため, 計測点群の大部分を占める床面 や 点密度が小さい部分点群,スポット割れ等の外れ値の除
円錐と円柱の重なり部分の体積を求める問題です すぐに回答を! 質問 No 閲覧数 1399 ありがとう数 2 気になる数 円柱と球と円錐の関係 数学・化学講師 佐藤学による受験生に 今日は円柱と球と円錐の関係について。皆さん、円柱と球と円錐の体積比はどうなる152 円柱と円柱 例題154 (教科書 練習問題8;3(2)) 2つの柱面x2y2 = a2, x2z2 = a2 (a >円柱 円錐 <体積 たいせき > ←3倍(×3) 1/3 倍(×1/3)→ (上図の→←を指しながら) 2つが同じ底面積,高さであることを確認。 「円柱の体積は円錐の体積の3倍,×3。円錐の体 積はその1/3 だから×1/3」 *AはBの 倍=BはAの1/ 倍 ことばの式には随時ルビふり 柱体の体積=(底面積)×
Safety How works Test new features Press Copyright Contact us Creators熊本大学数理科学総合教育センター 3(9)(立体の体積2) 球x 2y z 25 4a2 と円柱x y2 5 a の共通部分E の体積を求めよ. 解 x 2y z2 5 4a 2よりjzj 5 p 4a x2 y2 だから, E = n (x;y;z) x 2y2 5 a ;二円柱が交差する部分の体積 2円柱描画 共通部分描画 4頂点とする正方形となる。一辺の長さは 共通部分のみ描画 2つの直交している円柱 z2x2(a2 ① z2y2(a2 ② がある。 (1) 円柱①,②の共通部分の xy 平面に平行な平面z=tによる切り口は どのような図形か。また、切り口の面積を t の関数とし
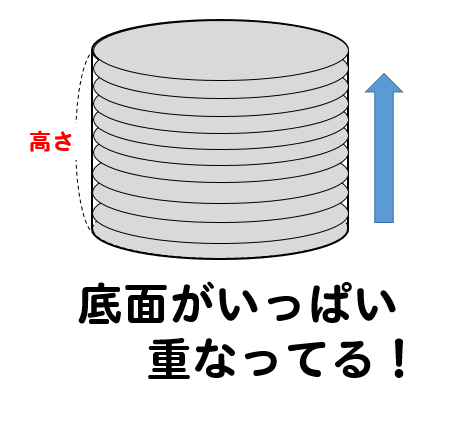



算数 円柱の体積の求め方 公式で確認 小学生向け 数スタ
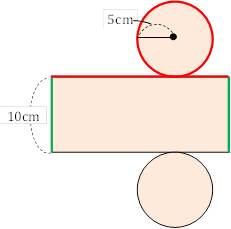



中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン
数学では2つの数量の関係について多く学びます。 中学1年では、「比例」と「反比例」について学びます。 「比例」は比較的すんなりと理解できるものの、「反比例」には苦手意識を持つお子さんは多くいます。 ここで反比例の意味・式・グラフについ0) で囲まれた立体の体積を求めて下さい。 解答例その1 題意の立体は(x,y)平面に関して対称なので、その体積V は(x,y)平面内の円x2 y2 ≤ a2 上で関数 √二重積分で共通部分の体積を求める問題 2つの円柱x^2y^2<=a^2,y^2z^2<=a^2の共通部分における立体の体積を求めよ。 これをx=rcosθ,y=rsinθとして積分し求めたいのですが、 上手く行きません。 よろしくお願いします。 数学 In=∫1→e(logx)^n・dx とおく。 In1を、Inで表してください。また、0<In<e/(n1



1
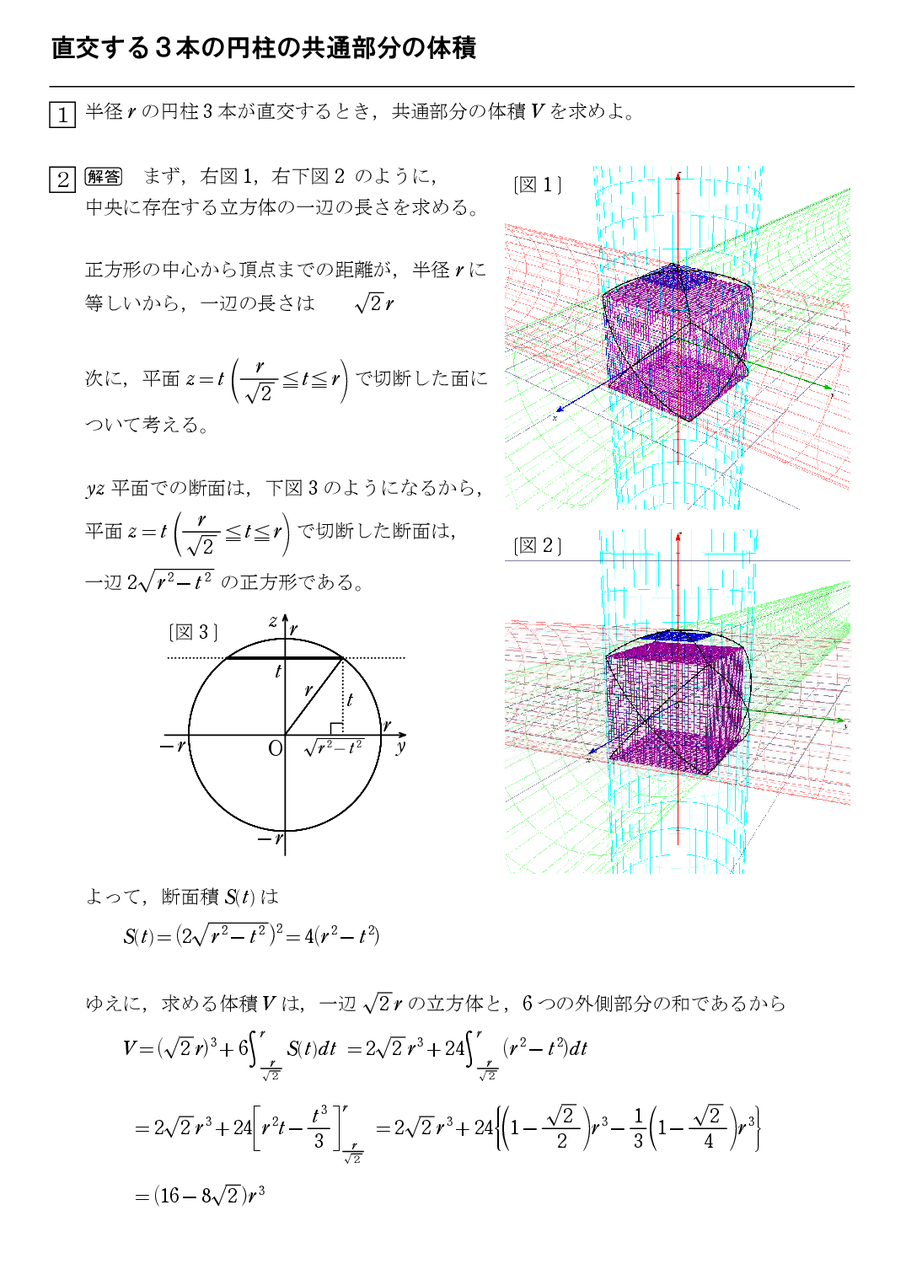



直交する3本の円柱の共通部分の体積 怜悧玲瓏 高校数学を天空から俯瞰する
(体積の計算) 立体の体積を求めるには,体積の微分が断面積になることを利用します. 円錐台であるから,実際には円柱の側面よりは狭い部分と広い部分があるが,積分に使うのは1次近似で,中央で見れば差し引き帳消しになると解釈できる 例題61 半径 の球の表面積は に等しい体積3 17年12月15日 19年2月8日 次もよくある問題で、柱体の共通部分の体積を求める問題です。 まずは円柱と円柱から。 より基本的な問題は数学Ⅱの体積の方にあります。 1. B (東北大) 空間において,半径が1で 軸を中心軸として原点から両側に無限それでは、円柱の体積問題をバッチリにするため演習問題に挑戦してみましょう! 円柱の演習問題(小学生) 次の円柱の体積を求めましょう。 解説&答えはこちら 答え $$7536(cm^3)$$ まずは底面積を求めましょう。 $$2\times 2\times 314=1256(cm^2)$$ 底面積が求まれば、高さをかけるだけ! $$1256\times




5 8 円柱を3等分した図形の体積と面積を求めるには さんすうがく



いろいろな立体の問題
小学6年生の算数 角柱や円柱の体積の求め方・公式 問題プリント 小学6年生の算数角柱や円柱の体積の求め方・公式の練習問題プリントを無料ダウンロード・印刷 (プリント5枚) 小学6年生の算数 図形の拡大と縮小拡大図と縮図 問題プリント 小学6年生の算数図形の拡大と縮小底面が直径10cmの円・高さがcmの円柱の体積をY くりぬいた四角柱と円柱の重なり(底面が直径10cmの円・高さが10cmの円柱)の体積をZ とします。 求める体積は、 =U-X-Y+Z =6000-785 =5215cm 3 なお、U-(X+Y-Z)としても同じことですね。 (解法3)真正面から見た図で考えて解きます(真横Viviani曲線 球と円柱の共通部分の体積 ***** 慶応大91年の問との相違点は球のふくらみ部分(上図の赤い部分)が付け加わったことです。 このことで計算は格段に難度を増しています。東工大04年、東京大03年、東京大94年などの問 いで使った方法を璮いることとなります。 図1 平面z=tによる切断




円柱を2つ重ねた立体の表面積の求め方 Qikeru 学びを楽しくわかりやすく




切断された物体の体積 画像のように 半径aの円柱を切断 その体積を求めた Okwave
円柱の先端を浮輪内周に沿う円柱状の刃で載 り取った立体で、乱視用の円柱レンズに相当する。1 比較のため先ず西洋流の定積分を求あよう。定積分の 簡明化のため、戊積一i\Gamma 所の寸法を 2 倍 (体積は 8 倍) した立体で考えて、戊積四 lF 所のため後で 213 体積、曲面積 131 体積の計算 宿題131 1) 二つの円柱x2 y2 • a2, y2 z2 • a2 の共通部分の体積を求 めよ。(変数変換は必要ない) 2) 円柱面x2 y2 = a2, 平面z = 0, 曲面z = x2 y2 で囲まれた領域の体積 を求めよ。 48 3) 円柱面x2 y2 = a2 の円柱面x2 z2 = a2 の内部にある部分の曲面積を 求めV = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 面積 ヘロン
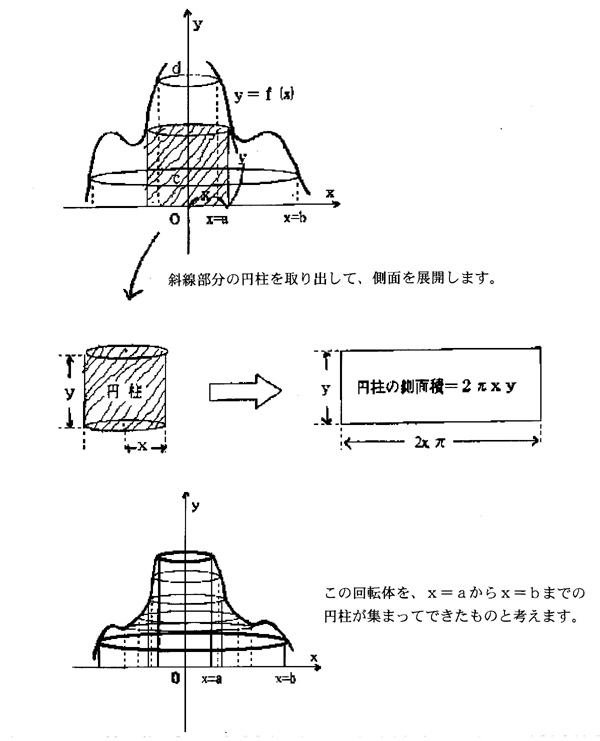



高校数学 バームクーヘン積分



3 13 体積の計算
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy &円柱の体積の求め方を確認したところで、円柱の体積の公式についてふれておきましょう。 ある円柱において、底面の円の半径を r 、高さを h 、その円柱の体積を V とすると、V=πr 2 h問 3 70 (体積の計算) 2 つの円柱 の共通部分 の体積 を求めよ. 次 314 曲面積 上 3 多重積分 前 312 演習問題 ~ 多重積分の積分変数の変換



5 8 円柱を3等分した図形の体積と面積を求めるには さんすうがく




非回転体 交差する円柱の共通部分 Steinmetz Solid 理系のための備忘録
北海道大学 理系 a,bを正の実数とする。 xyz空間内の2点 A(a,0,0),B(0,b,1)を通る直線を lとし、直線lを z 軸のまわりに一回転して得られる曲面をMとする。 1P(x,y,z)を曲面M上の点とする。このとき x,y,zが満たす関係 式を求めよ。 2曲面Mと2つの平面 z = 0と z = 1で囲まれた立体の体積を求直交する円柱 半径が1の2つの円柱が直交する物体がある。この共通部分の体積v 1 はいかほど か? また、半径が1の3つの円柱が1ヶ所で互いに直交する物体がある。この共通部分 の体積v 2 はいかほどか? この問いかけに対して、平成21年10月4日付けで、ペントミノさんが解答を寄せられた正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の体積 四角錐台の体積 くさび形の体積 角錐台の体積 角錐の体積 直円柱の体積 一部が欠けた直円柱の体積 中空円柱の体積 斜切円柱



算数の問題です 1 図の立体は 円柱を半分に切った形です この立体の体積は何 Yahoo 知恵袋




重積分5 三つの交差する円柱の領域の体積 数学 微分積分学 Mathematics Youtube
二重積分で共通部分の体積を求める問題 2つの円柱x^2y^2<=a^2,y^2z^2<=a^2の共通部分における立体の体積を求めよ。 これをx=rcosθ,y=rsinθとして積分し求めたいのですが、 上手く行きません。 よろしくお願いします。次のような角柱や円柱の体積を求めましょう。 ① ② 式 式 右のような四角柱の体積を 求めましょう。 右のような三角柱の体積を 求めましょう。 角柱と円柱の体積 名 前 6年 組 教科書110〜113ページ) 答え 答え 6cm 2cm 4cm 6cm 4cm 5cm 5cm 12cm 6cm 12cm 10cm 15cm (教科書13〜22ページ) ①6角柱と円柱の体積 問題6(ワード:174kb) 解答6(ワード:194kb) 7およその面積 問題7(ワード:164kb) 解答7(ワード:507kb) 8比と比の値 問題8(ワード:195kb) 解
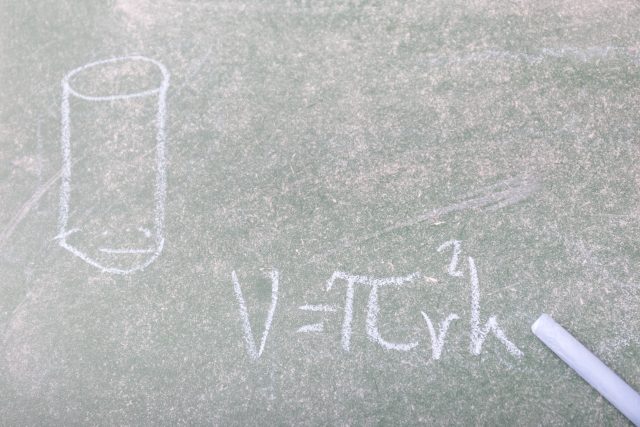



中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン



桜蔭中学過去問題演習
体積・表面積⑵ 角柱 1 ステップ1 角柱の体積 1 図1のように、地面に置かれた図形があります。この図形を、図2のよ うに真上に移動させます。このとき図形が動いてできたあとは、図3のよ うな立体になります。この立体を、「柱 ちゅう 」といい、もとの図形が三角形な ら「三角柱」、四角体積の導出 円柱の体積 \( V \) は\V = 8 \iint_D \sqrt{a^2 x^2} \\D = \{ (x,y) \mid x^2 y^2 \leqq a^2 , x \geqq 0 , y \geqq 0 \ \} \で求めることができる。 ここで積分領域 \( D \) が円なので極座標に置きたくなるが、極座標にしてしまうと \( f(x,y) \) の部分が計算しにくくなるので今回は極座標には変換しない。 2本単元で扱う角柱と円柱の体積は,学習指導要領には以下のように位置づけられている。 第6 学年「B量と測定」 (3)図形の体積を計算によって求めることができるようにする。 ア 角柱及び円柱の体積の求め方を考えること。 立体については,第4学年で直方体・立方体を学習したのに続き




非回転体 交差する円柱の共通部分 Steinmetz Solid 理系のための備忘録




非回転体 交差する円柱の共通部分 Steinmetz Solid 理系のための備忘録
不等式で表された立体の体積、直交する円柱の共通部分の体積 スポンサーリンク 高校数学Ⅲ 積分法の応用(面積・体積・長さ) 検索用コード x0,x²y²1,0 z y²\ で表される立体の体積Vを求めよ$ 立体の形状をイメージしようとするのは無理がある正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の体積 四角錐台の体積 くさび形の体積 角錐台の体積 角錐の体積 直円柱の体積 一部が欠けた直円柱の体積 中空円柱の体積 斜切円柱Jzj 5 p 4a2 x2 y o と表される.ゆえに, Vol(E) = ZZZ E dxdydz = ZZ fx2y25a 2g dxdy
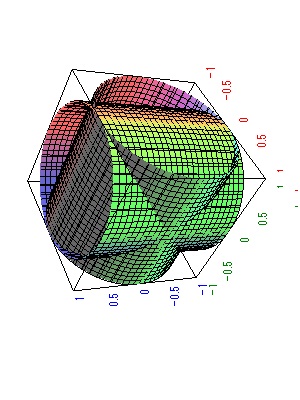



直交する2円柱を作る コ コ ロで遊ぶ算数教室




直交する円柱が作る立体とその体積 小6算数 萌えとかプログラミングとか
中学校報告書1において,円柱の体積を求 める問題の正答率は423 %だった。さらに, 国立教育政策研究所が出している同調査の調 査結果のポイント2では,「空間図形の性質 を考察する際に,見取図,展開図,投影図な体積 角柱または円柱の底面積をS、高さをh、体積をVとすると、 = と表わされます。 また、錐体の体積は、 = と表されます。 球の表面積、体積 半径rの球の表面積をS、体積をVとすると2つの円錐の共通部分の体積 xyz空間内に点A (2, 0, 2)とB (2, 0, 2) がある.また,点Pはxy平面上の原点を中心とする半径2の円の周と内部を自由に動く点とする。 線分APの通過する範囲をK,線分BPの通過する範囲をLとするとき,KとLの共通部分の体積を求めよ
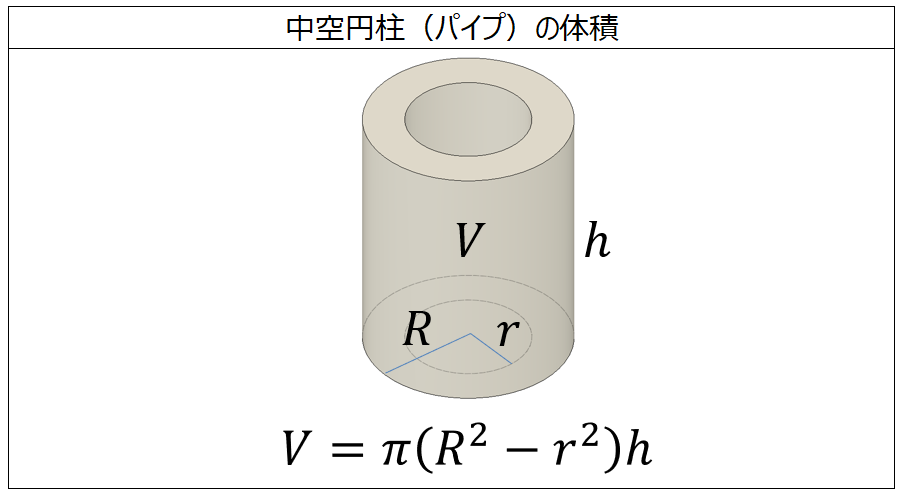



体積の計算 中空円柱 パイプ 製品設計知識




算数 円柱の体積の求め方 公式で確認 小学生向け 数スタ
特に,体積が一辺 r r r の立方体 4 4 4 個ぶんちょっとということは感覚的に納得できます。 高校数学では,そもそも曲面の面積ってなんだ?って感じなので,表面積の導出に関しては一部厳密でない表現も含まれています,ご了承ください。 体積の証明 球の体積公式を証明します。数学Ⅲで




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
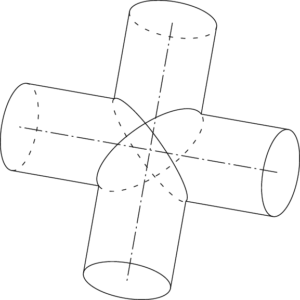



円柱の共通部分の体積 非回転体の体積 大学入試数学の考え方と解法




非回転体 交差する円柱の共通部分 Steinmetz Solid 理系のための備忘録



球x 2 Y 2 Z 2 A 2と円柱 X 2 Y 2 Axの共通部分の Yahoo 知恵袋




算数 円柱の体積の求め方 公式で確認 小学生向け 数スタ




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン



Http Www Shimanet Ed Jp Minami Link Homepage Naga005 Grapes 001 Enchuu3ko Pdf




直交する3本の円柱の共通部分の体積 怜悧玲瓏 高校数学を天空から俯瞰する



直交する3円柱を作ってみましょう オモシロ算数



Nekodamashi Math Blog Ss Blog Jp 17 11 03




円柱 円錐 球のcの求め方と公式 高校生向け受験応援メディア 受験のミカタ




2つの円柱が重なる部分の表面積を求める問題の別解を考えました あってないようですが Clear
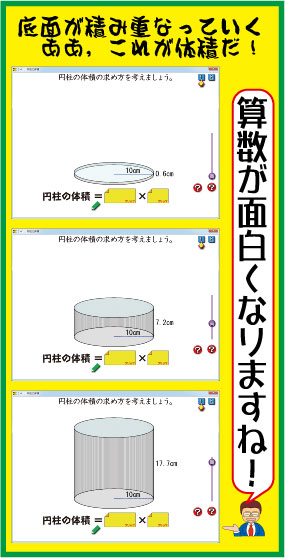



6年の円柱体積のソフト さくら社




Descubre Como Resolverlo En Qanda



Http Www Shimanet Ed Jp Minami Link Homepage Naga005 Grapes 001 Enchuu2ko Pdf
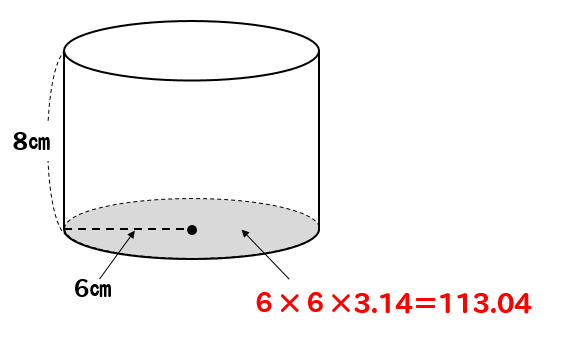



算数 円柱の体積の求め方 公式で確認 小学生向け 数スタ
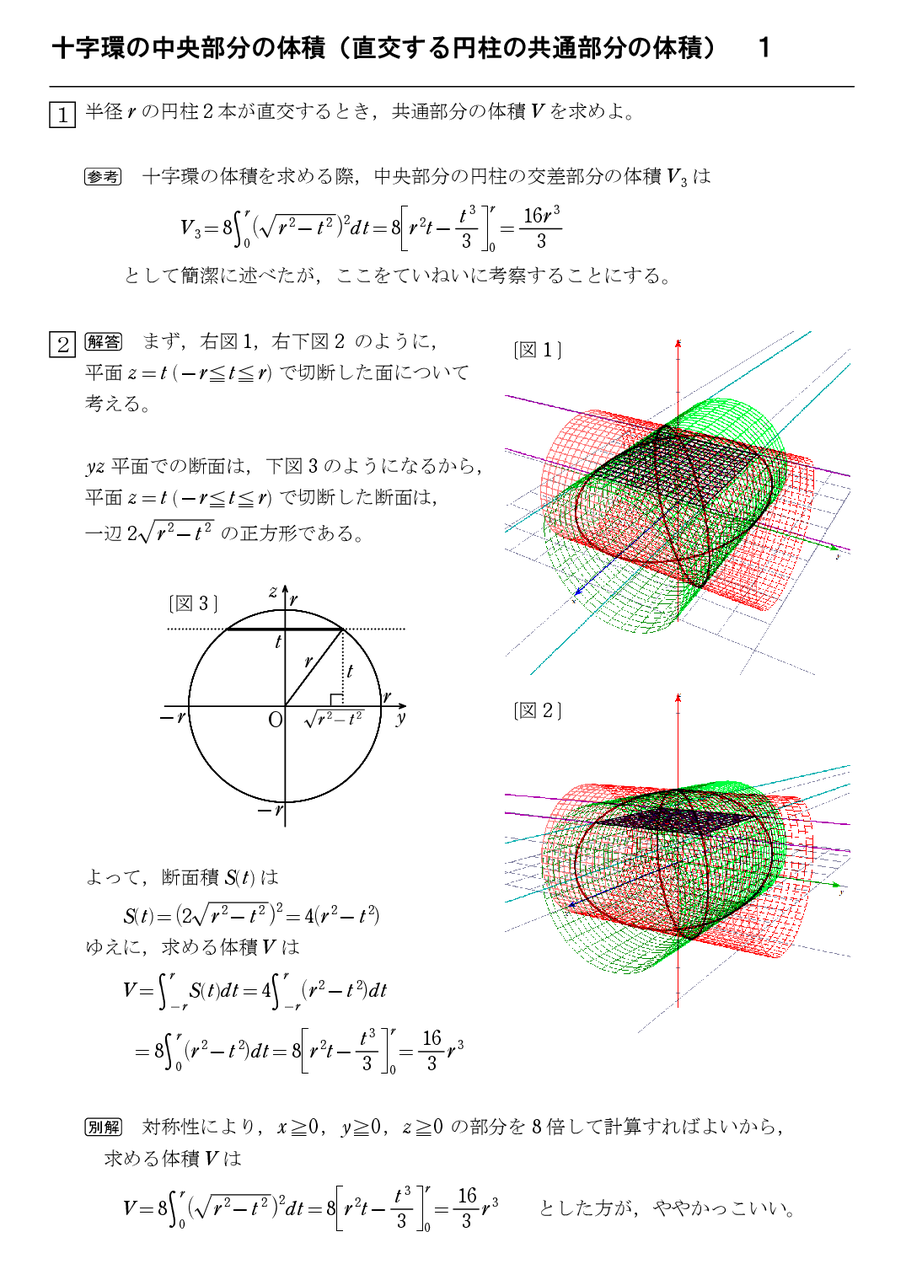



直交する3本の円柱の共通部分の体積 怜悧玲瓏 高校数学を天空から俯瞰する



研究




2つの直交する円柱の共通部分の体積を求めよ Youtube
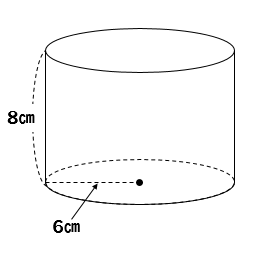



算数 円柱の体積の求め方 公式で確認 小学生向け 数スタ
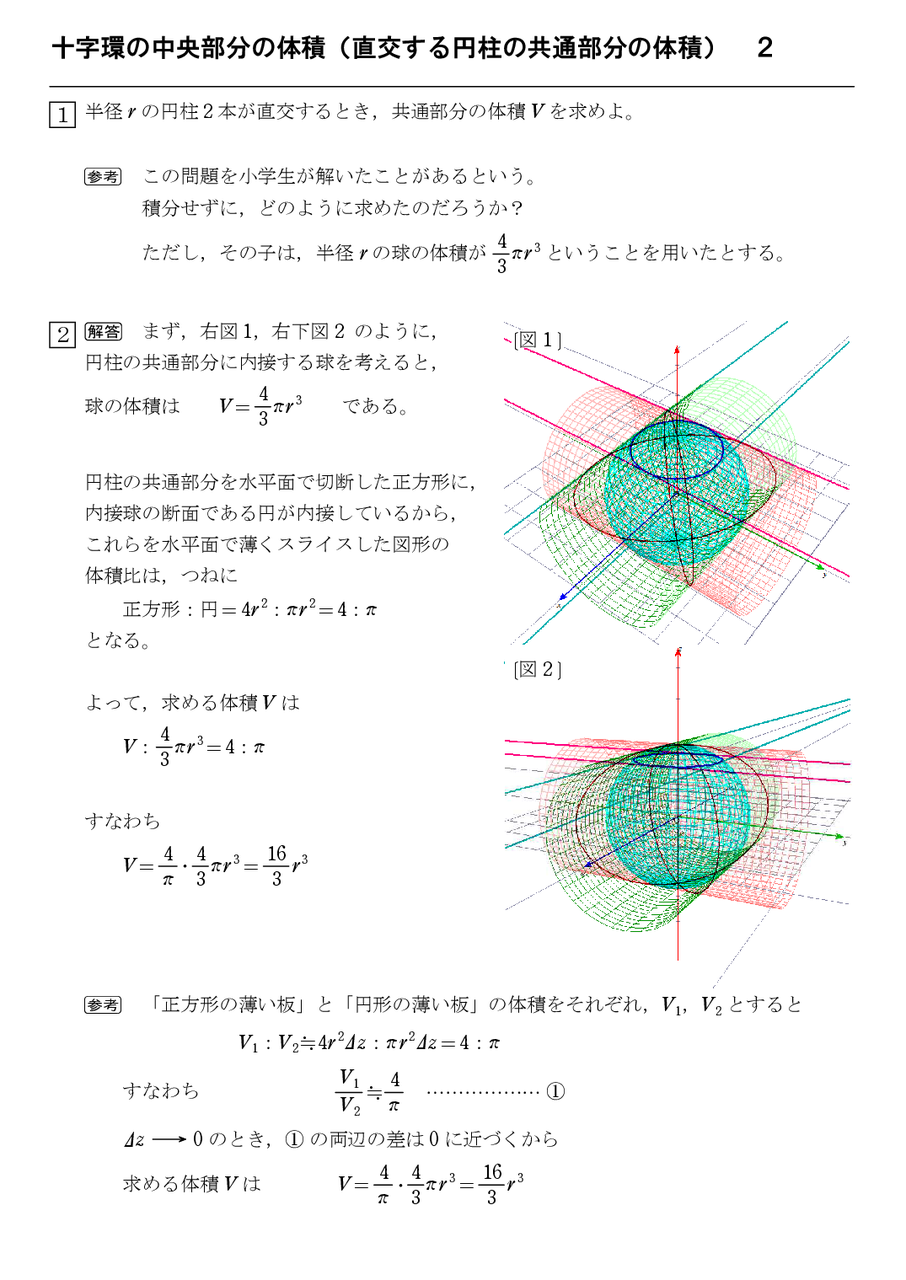



直交する3本の円柱の共通部分の体積 怜悧玲瓏 高校数学を天空から俯瞰する




アサの一題 数学 非回転体の体積8 円柱の重なりの体積 Youtube




円柱と球の共通部分の表面積 球x 2 Y 2 Z 2 1と円柱x 2 Y 2 Xとの共通 数学 教えて Goo




ねこ騙し数学



いろいろな立体の問題




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




直交する3本の円柱の共通部分の体積 怜悧玲瓏 高校数学を天空から俯瞰する



Http Www Shimanet Ed Jp Minami Link Homepage Naga005 Grapes 001 Viviani All Volume005 Pdf
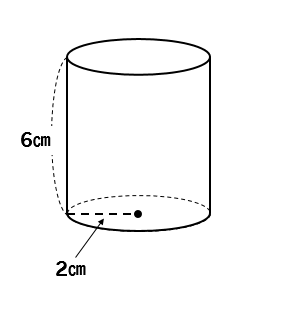



算数 円柱の体積の求め方 公式で確認 小学生向け 数スタ




3つの直交する円柱の共通部分の体積 数学の偏差値を上げて合格を目指す



半径aの2つの直円柱が直交しているとき 共通部分の体積を求めな Yahoo 知恵袋
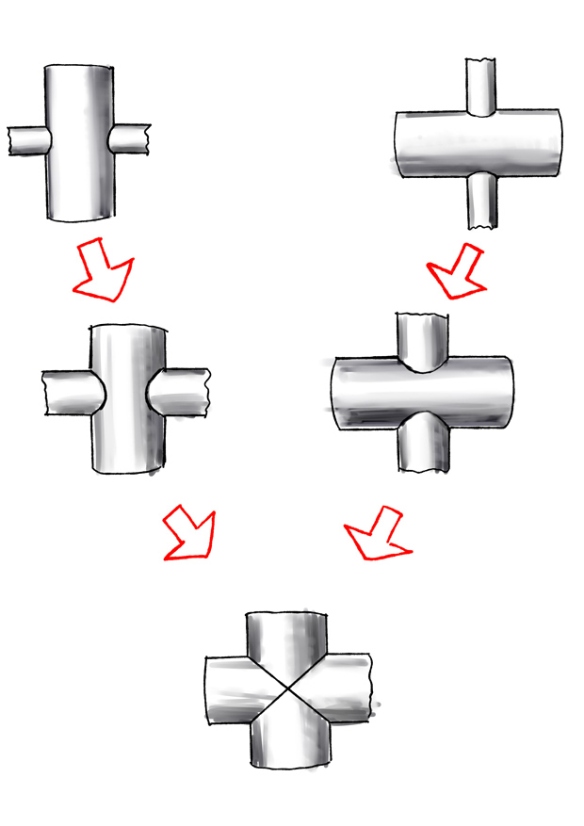



直交する円柱が作る立体とその体積 小6算数 萌えとかプログラミングとか




高校数学 不等式で表された立体の体積 直交する円柱の共通部分の体積 受験の月




ヴィヴィアーニカーブ こうばしいブログ




3つの直交する円柱の共通部分の体積 数学の偏差値を上げて合格を目指す



Http Www Shimanet Ed Jp Minami Link Homepage Naga005 Grapes 001 Enchuu3ko Pdf




ねこ騙し数学



Http Www Shimanet Ed Jp Minami Link Homepage Naga005 Grapes 001 Enchuu2ko Pdf




回転体の体積と表面積 中学数学の計算の求め方 リョースケ大学
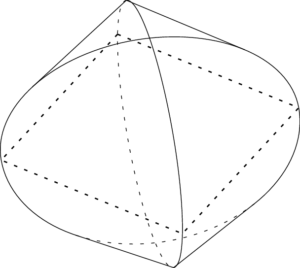



円柱の共通部分の体積 非回転体の体積 大学入試数学の考え方と解法



斜めに切った円柱や角柱の体積を求める方法 中学受験ー算数解き方ポータル
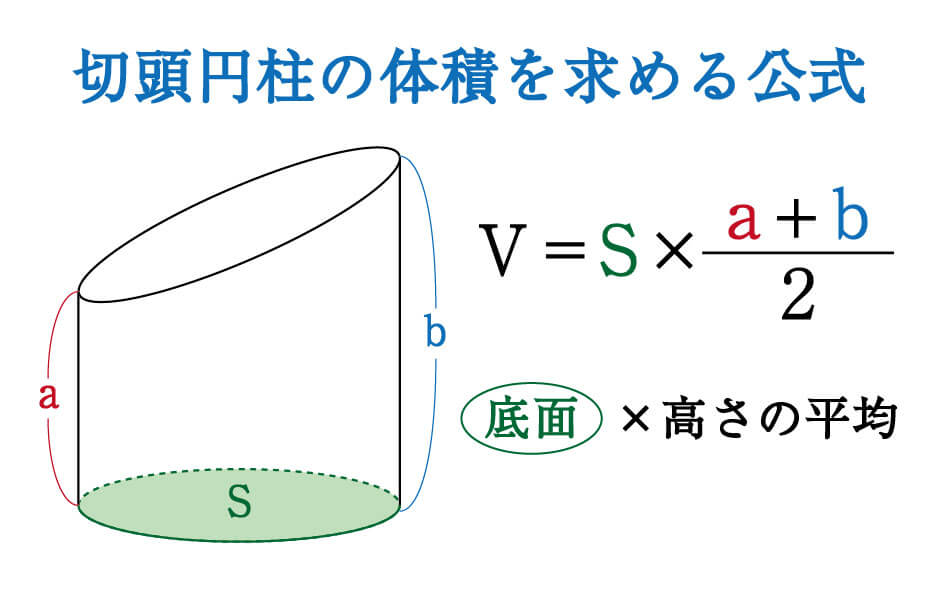



数学 斜めに切断された円柱 四角柱の体積は こう解くべし 受験の秒殺テク 6 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



桜蔭中学過去問題演習



いろいろな立体の問題
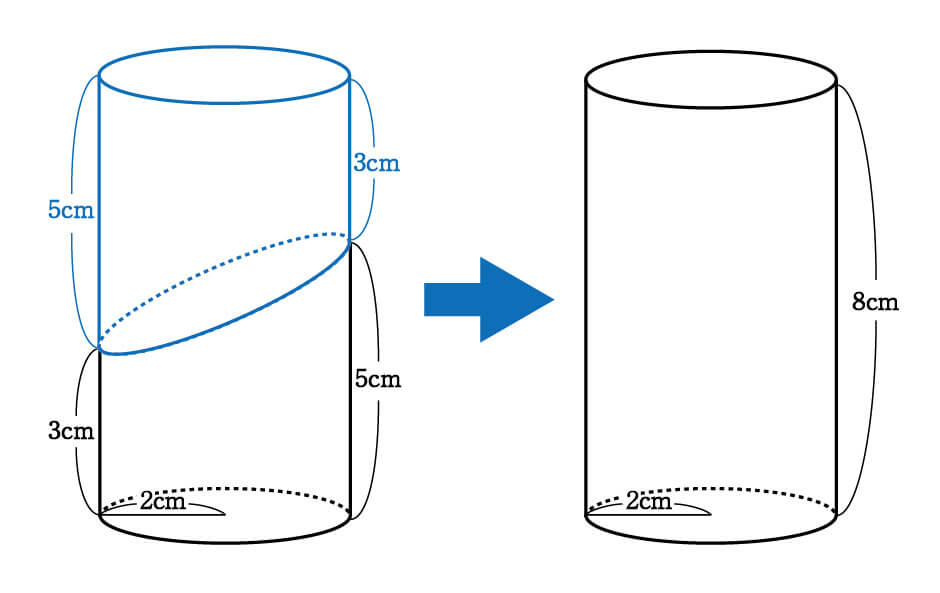



数学 斜めに切断された円柱 四角柱の体積は こう解くべし 受験の秒殺テク 6 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



直交した2つの円柱の共通部分の体積を計算したいのですが 添付図 Yahoo 知恵袋



研究




非回転体 交差する円柱の共通部分 Steinmetz Solid 理系のための備忘録
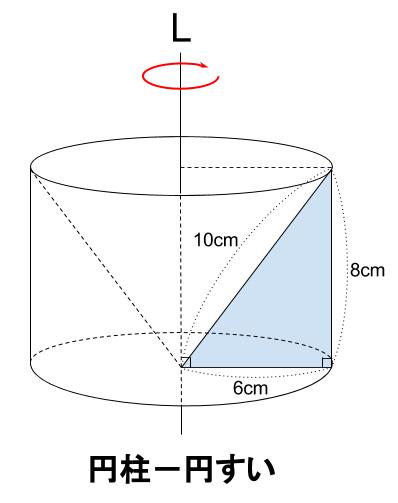



中学数学 回転体 その2 中学数学の無料オンライン学習サイトchu Su



直交する円柱




円錐と円柱の重なり部分の体積を求める問題です Okwave
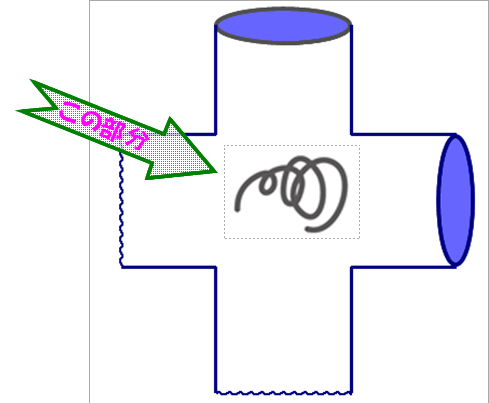



立体感覚up なるほど算数 数学



直交する円柱
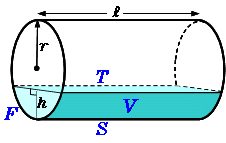



一部が欠けた直円柱の体積 高精度計算サイト




中学数学 円柱の体積の求め方と公式 塔をモチーフ なぜか分かる はかせちゃんの怪しい研究室




多次元空間へのお誘い 8 通用しない一般常識 とね日記



桜蔭中学過去問題演習



3
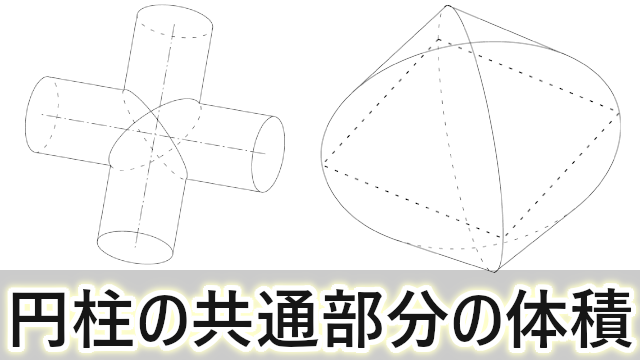



円柱の共通部分の体積 非回転体の体積 大学入試数学の考え方と解法




2つの円柱が重なる部分の表面積を求める問題の別解を考えました あってないようですが Clear




簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



Http Www Din Or Jp Saigou Math Sagi24 Pdf



1




非回転体 交差する円柱の共通部分 Steinmetz Solid 理系のための備忘録
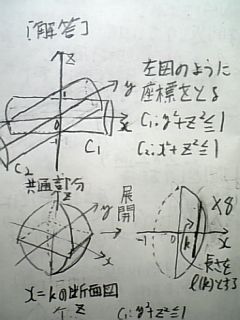



直交する円柱の共通部分の体積と表面積 わんこら日記




3つの直交する円柱の共通部分の体積 数学の偏差値を上げて合格を目指す




重なっているところの体積を Aからaで解くのかと思ったら切り方とかってかかれていて Clear




半径aの円柱を平面z Yで切った時 Z 0 の体積と表面積の求め方がわかり 大学 短大 教えて Goo



ユキコさんからの質問



山口大学 工 理 教育 14年問題2 Suugaku Jp




重積分4 二つの交差する円柱の領域の体積 数学 微分積分学 Youtube




回転体の体積と表面積 中学数学の計算の求め方 リョースケ大学




円柱の高さと球の高さって同じってことですよね 教えてください 中学校 教えて Goo



1



Www Pref Hiroshima Lg Jp Uploaded Attachment Pdf



いろいろな立体の問題
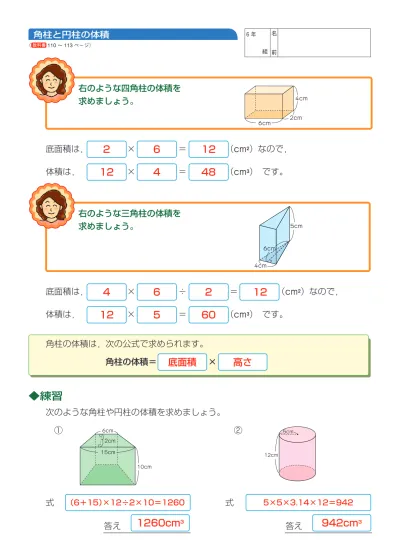



角柱と円柱の体積 6 年 名 教科書 ページ 組 前 右のような四角柱の体積を求めましょう Cm Cm Cm 底面積は 2 6 12 Cm 2 なので 体積は 12 4 48 Cm 3 です




直交する円柱が作る立体とその体積 小6算数 萌えとかプログラミングとか
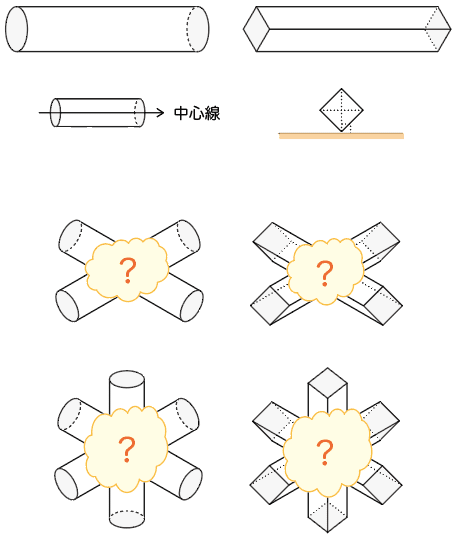



円柱どうし 角柱どうしの交わり 大森 武 Note
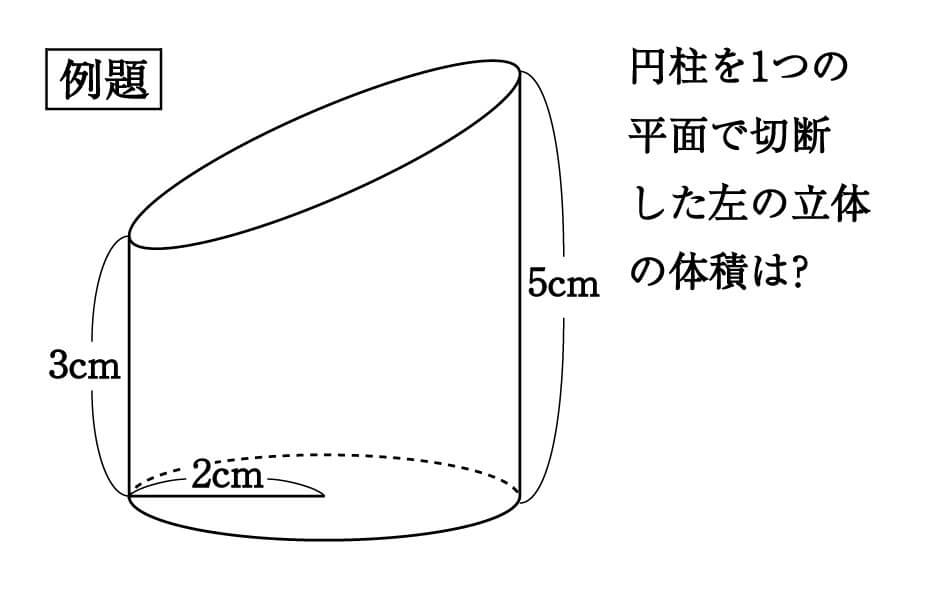



数学 斜めに切断された円柱 四角柱の体積は こう解くべし 受験の秒殺テク 6 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




高校積分で 二つの交差する円柱の領域の体積を求めます 数学 微分積分 Youtube



0 件のコメント:
コメントを投稿